Experimental Physical Chemistry: PUNTO DE CONGELACIÓN Y EBULLICIÓN

El punto de congelación de un líquido es la temperatura a la que dicho líquido se solidifica debido a una reducción de temperatura. El proceso inverso se denomina punto de fusión.
Para la mayoría de sustancias ambas temperaturas son iguales. Por ejemplo para el mercurio, cuya temperatura de fusión y de congelación es 234,32 K (−38,83 °C). Sin embargo otras sustancias como el Agar-Agar tienen distintas temperaturas para la fusión y la congelación siendo que se vuelve líquido a 85 °C y sólido a una temperatura entre 32 °C y 40 °C; a este fenómeno se le conoce como histéresis.
En el caso del agua, el punto de fusión y de congelación es el mismo: 0 °C. Esto es en presencia de núcleos de cristalización en el líquido, ya que si éstos no están presentes, el agua líquida puede enfriarse hasta −42 °C sin que se produzca la congelación en un proceso llamado superenfriamiento.

La sobrefusión (a veces llamada superenfriamiento o subfusión) es el proceso de enfriar un líquido por debajo de su punto de congelación sin que este se haga sólido

Un líquido que esté por debajo de su punto de ebullicion y fusion, cristalizará en presencia de un cristal semilla o núcleo alrededor del cual se pueda formar una estructura cristalina. Sin embargo, a falta de núcleos, se puede mantener el mismo estado hasta llegar a la temperatura en la que se produce nucleación homogénea del cristal. La nucleación homogénea se puede producir por encima de la transición vítrea cuando el sistema es un sólido amorfo, esto es, no es cristalino.
El punto de congelación del agua es de 273,15 K (0 °C), pero se puede superenfriar a presión ambiental hasta su nucleación homogénea, a casi 231 K (−42 °C).^[1] Si se enfría a un ritmo del orden de -10⁶ K/s, se puede evitar la nucleación cristalina y el agua se convierte en un vidrio. Su temperatura de transición vítrea es muy inferior y difícil de determinar, pero hay estudios que la estiman en unos 165 K (−108 °C).^[2] El agua vítrea se puede enfriar hasta aproximadamente 150 K (−123 °C).^[1] En el rango de temperaturas entre 231 K (−42 °C) y 150 K (−123 °C), los experimentos sólo han logrado hielo cristalino.
En los estratos y los cúmulos a menudo existen gotas de agua superenfriada. Cuando son golpeadas por el viento de un avión que pasa, cristalizan abruptamente formando hielo. Esto causa problemas en el vuelo, por lo que los aviones que van a viajar en esas condiciones deben tener un sistema antihielo.
El equivalente al superenfriamiento para el proceso de fusión de los sólidos es mucho más difícil, por lo que un sólido casi siempre se funde a la misma temperatura para una cierta presión. Sin embargo, es posible supercalentar un líquido por encima de su punto de ebullición sin que se haga gaseoso.

Historia

El químico francés François-Marie Raoult estudió las propiedades de las disoluciones con diversos disolventes, como agua, benceno o ácido acético, y publicó sus resultados en 1882.^[5] En ese trabajo explicó que los solutos disminuyen las temperaturas del punto de congelación de las disoluciones y que la variación experimentada de la temperatura sólo es proporcional a la cantidad de soluto disuelto expresada en fracción molar y no depende de su naturaleza.
Con esas investigaciones, Raoult puso a disposición de los químicos un nuevo método analítico de determinación de masas moleculares de sustancias disueltas. Así, la ley de Raoult del descenso crioscópico se convirtió en el método más útil para la determinación de masas moleculares de sustancias orgánicas, especialmente tras haber sido mejorado por el alemán Ernst Otto Beckmann. Los trabajos de Raoult también fueron utilizados, entre otros, por Jacobus Henricus van 't Hoff y Wilhelm Ostwald, como apoyo para la hipótesis de la disociación electrolítica en las disoluciones, además de permitir a Svante August Arrhenius disponer de pruebas experimentales para su teoría de la disociación electrolítica.
Jacobus Henricus van 't Hoff realizó un estudio sistemático de las propiedades coligativas de las disoluciones publicado en 1885.^[6] En ese trabajo observó que un extenso grupo de disoluciones no obedecía las leyes simples que había descubierto Raoult, incluso variando las diluciones. Esas anomalías, que eran excepcionalmente elevadas en el caso de muchos electrolitos, condujeron a van 't Hoff a introducir el llamado «factor de van 't Hoff», un factor empírico que intenta corregir la ecuación de Raoult para poder aplicarla en electrolitos.
Raoult también dio nombre a esa nueva técnica analítica, a la que llamó crioscopia, a partir de las palabras griegas κρυóς (kryos, que significa frío) y σκοπέω (skopein, que significa mirar, examinar u observar).

Causas del descenso crioscópico

Termómetro diferencial de Beckmann.

El descenso crioscópico se puede explicar a partir de la variación de entropía que se produce durante el cambio de fase.^[8] La entropía es una medida del desorden del sistema. Así, un sólido puro está más ordenado que un líquido puro, y por lo tanto, este último tiene una mayor entropía, un mayor desorden. El desorden es debido a que las partículas (moléculas, átomos o iones) de un sólido ocupan una posición fija y solo vibran alrededor de esa posición. Por el contrario, en un líquido las partículas están en movimiento y no tienen una posición determinada. Una disolución líquida tiene más desorden que un líquido puro ya que en la disolución, además de las partículas del disolvente en movimiento, también se encuentran las partículas de soluto en movimiento, lo que hace que el sistema esté más desordenado. Podemos ordenar los sistemas de más a menos entropía:
$S_{dis} > S^*_l > S^*_s \,$ La variación de entropía que se produce durante un cambio de estado, en este caso de líquido a sólido, viene acompañada de una variación de entropía, que es la diferencia de entropía entre los estados final e inicial. En el caso de un disolvente puro, la variación corresponde a la diferencia de entropía entre el disolvente sólido y el disolvente líquido y se le llamará ∆S^*_f; en el caso de una disolución, la variación de entropía es la diferencia entre la entropía del disolvente sólido y la disolución, y se le llama ∆S_f. Esta última es superior a la primera porque la disolución tiene más entropía que el disolvente líquido. Por lo tanto:
$\Delta S^*_f > \Delta S_f \,$ Por otro lado, la congelación es una transición de fase de primer orden, es decir, tiene lugar con una variación brusca de entropía de forma prácticamente reversible a la temperatura y presión de equilibrio. Así, se puede relacionar la variación de entropía que se produce con la entalpía de cambio de fase (calor latente), ∆H_f, y la temperatura, T_f, según la ecuación:^[2] ^[3]
$\Delta S_f = \frac {q_{rev}}{T} = \frac {\Delta H_f}{T_f}$ Dado que la variación de la entalpía, ∆H_f, es constante, tanto en el paso del disolvente líquido a sólido como del disolvente de la disolución a sólido, se obtiene que si la variación de entropía es mayor en el caso de la disolución, la temperatura del cambio de fase deberá ser menor para que el segundo miembro de la igualdad aumente para igualar la mayor variación de entropía de la congelación del disolvente de la disolución. Matemáticamente se demuestra:
$\Delta S^*_f < \Delta S_f \,$
$\frac {\Delta H_f}{T^*_f} < \frac {\Delta H_f}{T_f}$
$T_f < T^*_f \,$ Por tanto, las temperaturas de congelación de las disoluciones son siempre menores que las del disolvente puro debido a que la disolución tiene más entropía, más desorden, que el disolvente líquido puro. A mayor concentración de soluto, mayor desorden, mayor entropía en la disolución y, por lo tanto, menor temperatura de congelación y mayor descenso crioscópico.^[9]

Ecuaciones

Disoluciones diluidas de no electrolitos

Descenso crioscópico experimentado por una disolución acuosa de etanol en función de la molalidad, donde se observa la curva experimental en rojo y la recta que se obtiene de aplicar la ecuación de Raoult en azul, y que, en el caso del etanol, es válida hasta concentraciones de aproximadamente 3 molal.^[1]

Raoult, de forma experimental, llegó a deducir lo que se conoce como Ley de Raoult del descenso crioscópico para el caso del descenso crioscópico de disoluciones diluidas con solutos que no se disocian, es decir, no electrolitos. La ecuación de dicha ley es:
$\triangle T_c = k_f \cdot m$ donde:

ΔT_c es la diferencia entre la temperatura de congelación del disolvente puro y la temperatura de congelación de la disolución.
k_f es la constante crioscópica, una constante que es característica del disolvente.
y m es la molalidad del soluto, es decir, los moles de soluto por kilogramo de disolvente. La concentración se expresa en molalidad porque es más práctico a la hora de realizar medidas, aunque para ser exactos se debería expresar en función de la fracción molar, como lo demostró Raoult.^[5]

Disoluciones diluidas de electrolitos

Descenso crioscópico experimentado por una disolución acuosa de cloruro de calcio en función de la molalidad.^[1]

Las anomalías descubiertas por Jacobus Henricus van 't Hoff, que eran excepcionalmente elevadas en el caso de muchos electrolitos, le condujeron a introducir el llamado factor de van't Hoff. Se trata de un factor empírico simbolizado por i que se define como el cociente entre el valor experimental de la propiedad coligativa media y el valor teórico que se deduce de las ecuaciones de Raoult.
$i = \frac {\Delta T_b (exp)}{\Delta T_b (teor)} = \frac {\Delta T_b (exp)}{k_b \cdot m}$ De esta forma, la nueva ecuación para el descenso crioscópico tomó la siguiente forma:
$\Delta T_c = i \cdot k_c \cdot m \,$ El factor i fue explicado por el químico sueco Svante August Arrhenius cuando desarrolló entre 1883 y 1887 la teoría de la disociación electrolítica, según la cual las moléculas de los electrolitos se disocian en mayor o menor extensión en iones cargados eléctricamente, capaces de transportar la corriente eléctrica, existiendo un equilibrio entre las moléculas no disociadas y los iones. Por tanto, en disolución hay más partículas que las que se han disuelto, ya que estas se rompen, se disocian, en partes más pequeñas. El ascenso ebulloscópico, como el resto de propiedades coligativas, depende del número total de partículas en disolución, de manera que en una disolución de electrolitos tendremos más partículas que las disueltas, las cuales se han de tener en cuenta para calcular la molalidad total. Por ejemplo, se puede suponer un electrolito binario como el cloruro de calcio, CaCl₂, que alcanza el equilibrio de disociación en agua según la siguiente ecuación:
$CaCl_2 \rightleftharpoons Ca^{2+}_{(aq)} + 2 Cl^{-}_{(aq)}$ En disolución, por tanto, hay más partículas que las disueltas inicialmente porque parte de estas se han disociado en iones.^[3] En la figura se observa que los datos experimentales se desvían mucho de la predicción de la Ley de Raoult.

Disoluciones reales

Descenso crioscópico experimentado por una disolución acuosa de D-glucosa en función de la molalidad.^[1]

La fórmula de Raoult del descenso crioscópico sólo da valores iguales a los experimentales cuando las disoluciones son muy diluidas. Para aplicarla a disoluciones reales, donde la concentración es mayor, hay que usar una ecuación que se obtiene en la demostración termodinámica antes de simplificarla y sustituyendo en ella la fracción molar del disolvente por la actividad de este, o bien el producto del coeficiente de actividad por la fracción molar.
$\int_{1}^{a^x_1} d \ln a^x_1 = \int_{T_f^*}^{T_f} \frac {\Delta H_f}{R \cdot T^2} \cdot dT$ La primera parte es una integral directa y para resolver la segunda hay que expresar la entalpía en función de la temperatura. Con esta ecuación se obtienen curvas (en negro en la figura de la derecha) que coinciden muy bien con los valores experimentales (en rojo).
Si no se tiene en cuenta la dependencia de la entalpía con la temperatura la integral resulta:
$\ln a^x_1 = \frac{\Delta H_f}{R} \left( \frac {1}{T_f^*} - \frac {1}{T_f} \right)$

El descenso crioscópico en la naturaleza

El agua marina

En el ártico, el agua se encuentra en estado líquido pese a encontrarse a temperaturas por debajo de los 0 °C.

La temperatura del agua de los océanos Ártico y Antártico, en sus respectivos inviernos, llega a bajar varios grados Celsius bajo cero, hasta un mínimo de -2 °C.^[10] El agua que se encuentra en contacto con la atmósfera alcanza temperaturas mucho más bajas y llega a congelarse; sin embargo, el agua líquida que queda por debajo no alcanza temperaturas tan bajas, pero sí que se encuentra a uno o dos grados bajo cero. La razón por la cual permanece en estado líquido es la concentración de sales disueltas (unos 35 g de sales, principalmente cloruro sódico, por kg de agua) que disminuyen la temperatura de congelación del agua marina.
Se puede calcular de forma aproximada hasta que temperatura puede mantenerse el agua del mar sin llegar a congelarse. Suponiendo que todas las sales son cloruro de sodio (NaCl) y que la concentración es de 35 g por kg de disolvente, se tiene una molalidad de:
$m = \frac{m_2/M_2}{m_1} = \frac{\frac{35 g}{58,5 g/mol}}{1 kg} = 0,598 \; molal$ Dado que el cloruro de sodio es un electrolito fuerte, se supone que está completamente disociado y el coeficiente de van't Hoff toma el valor de 2, aunque ese valor límite sólo se alcanza para disoluciones muy diluidas.^[11] Conociendo que la constante crioscópica del agua vale 1,86 °C·kg/mol se puede calcular el descenso crioscópico como:
$\Delta T_c = i \cdot k_f \cdot m = 2 \cdot 1,86 \cdot 0,598 = 2,2 {}^\circ C$ Por lo que el agua del mar puede alcanzar una temperatura de -2,2 °C sin congelarse.

Seres vivos con anticongelantes

Los huevos de Malacosoma americanum contienen glicerol en una proporción del 35% de su peso seco.

Algunos animales evitan la congelación usando anticongelantes fisiológicos. Se trata de solutos elaborados o incorporados a sus líquidos corporales durante las estaciones frías, con los que incrementan la concentración total de solutos y reducen la temperatura de congelación. Muchos insectos, por ejemplo, producen concentraciones elevadas de glicerol, sorbitol o manitol durante el invierno. Es el caso, por ejemplo, de las larvas de invierno de Bracon cephi que tienen una temperatura de congelación que puede alcanzar los -17 °C durante el invierno, mientras que los individuos de verano sólo pueden alcanzar los -1 °C. También los huevos de invierno de la oruga Malacosoma contienen glicerol en una cantidad del orden del 35% de su peso en seco.^[12]
La Rana sylvatica, que vive en la mitad septentrional de Norteamérica, es capaz de prosperar en un clima subártico. Este animal puede hibernar, sobreviviendo a la congelación de entre el 35 y el 45% de su cuerpo. Para ello se sirve de proteínas especiales, urea acumulada en los tejidos y glucosa almacenada en el hígado para limitar la cantidad de hielo que se forma en su cuerpo y reducir así la contracción osmótica de las células.^[13] ^[14]
En el océano Antártico viven un centenar de especies del género Notothenioidea que sintetizan un tipo de proteínas con características anticongelantes que se disuelven en la sangre y que les permiten sobrevivir a temperaturas de hasta -1,8 °C. Estas proteínas tienen un mecanismo de funcionamiento que no se basa en el descenso crioscópico y una efectividad unas 500 veces mayor. Al parecer, estas se adhieren a los núcleos de cristalización del hielo que se forman inicialmente e impiden su crecimiento posterior.^[15] ^[16]

Aplicaciones

Científicas

Calorímetro de Beckmann.

La ecuación del descenso crioscópico de Raoult resulta muy útil para la determinación de masas moleculares de solutos. Conocidas las propiedades del disolvente, a partir del descenso crioscópico se deduce la molalidad y, a partir de esta, si se conoce la masa del soluto disuelta por kilogramo de disolvente, se puede obtener la masa molecular del soluto. Esta técnica es conocida como crioscopia y para llevarla a cabo y conseguir buenos resultados se necesita un termómetro que permita apreciar las centésimas de grado en la zona de la temperatura de congelación. Las determinaciones se han de realizar para distintas concentraciones y extrapolar los resultados para una dilución infinita, debido a que la ecuación de Raoult solo se cumple en ese caso. Dicha ecuación tiene la forma
$\Delta T_c = k_f \cdot m = k_f \cdot \frac{n_2}{m_1} = k_f \cdot \frac{m_2/M_2}{m_1}$ donde el subíndice 1 corresponde al disolvente y el 2 al soluto. n₂ es el número de moles de soluto, m₂ es la masa de soluto expresada en gramos, M₂ es la masa molecular de soluto, y m₁ es la masa del disolvente en kilogramos. Aislando M₂ queda:
$M_2 = \frac{k_f \cdot m_2}{\Delta T_c \cdot m_1}$ Otra aplicación científica de la crioscopia es la determinación de actividades de disolventes y solutos, tanto electrolitos como no. A partir de la ecuación del descenso crioscópico para disoluciones reales, se puede obtener directamente la actividad del disolvente que se puede relacionar con las actividades del soluto usando la ecuación de Gibbs-Duhem.

Anticongelantes

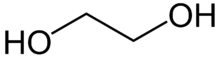
Estructura del etilenglicol

Eliminación del hielo de un avión mediante una disolución anticongelante.

La disminución de la temperatura de congelación de un disolvente debido a la presencia de un soluto se usa para evitar la solidificación del agua de refrigeración en los motores de combustión. En las regiones frías, donde la temperatura puede bajar de los 0 °C, se añaden sustancias al agua de refrigeración para rebajar su temperatura de congelación y evitar así que esta se congele, ya que, de producirse, el aumento del volumen del hielo podría romper el sistema de refrigeración. Las sales muy solubles en agua, como el cloruro de calcio, podrían ser apropiadas, ya que una disolución con un 30,5 % de CaCl₂ se congela a -50 °C. Sin embargo, no pueden usarse ya que corroen los metales. Como anticongelantes se usan disoluciones de etanol, etilenglicol o glicerina, ya que sus disoluciones al 36,5 % en peso, 39 % en volumen y 44,4 % en peso, respectivamente, congelan a partir de -25 °C. Si se desea disminuir más la temperatura de congelación se usan disoluciones de glicerina al 58 % que congelan a -50 °C.^[4] El más usado es el etilenglicol.^[17] ^[18] En los circuitos de refrigeración de paneles de energía solar el anticongelante que se utiliza es el propilenglicol.^[19]
El descenso crioscópico también se aprovecha para eliminar capas de hielo de las carreteras, autopistas y pistas de aeropuertos. Para ellos se lanza cloruro de sodio (NaCl) o de calcio (CaCl₂) sobre las placas de hielo, con lo que se disminuye la temperatura de congelación y se funden las placas de hielo. Una ventaja del cloruro de calcio es que, cuando este se disuelve, libera gran cantidad de calor que ayuda a fundir más el hielo. Para eliminar las capas de hielo que se forman sobre los aviones también se usa el etilenglicol.
En la construcción se usan anticongelantes para los hormigones en lugares donde las temperaturas son muy bajas y se congelaría el agua. No es posible usar grandes cantidades de anticongelante ya que provocaría problemas de corrosión. Los anticongelantes que se usan son sales, normalmente cloruro de calcio, CaCl₂, que en una proporción del 2 % reduce la temperatura de congelación a -5 °C

PUNTO DE EBULLICIÓN

El punto de ebullición es aquella temperatura en la cual la materia cambia de estado líquido a estado gaseoso, es decir hierve. Expresado de otra manera, en un líquido, el punto de ebullición es la temperatura a la cual la presión de vapor del líquido es igual a la presión del medio que rodea al líquido.^[1] En esas condiciones se puede formar vapor en cualquier punto del líquido.
La temperatura de una sustancia o cuerpo depende de la energía cinética media de las moléculas. A temperaturas inferiores al punto de ebullición, sólo una pequeña fracción de las moléculas en la superficie tiene energía suficiente para romper la tensión superficial y escapar. Este incremento de energía constituye un intercambio de calor que da lugar al aumento de la entropía del sistema (tendencia al desorden de las partículas que lo componen).
El punto de ebullición depende de la masa molecular de la sustancia y del tipo de las fuerzas intermoleculares de esta sustancia. Para ello se debe determinar si la sustancia es covalente polar, covalente no polar, y determinar el tipo de enlaces (dipolo permanente - dipolo inducido o puentes de hidrógeno).

Cálculo del punto de ebullición

El punto de ebullición normal puede ser calculado mediante la fórmula de Clausius-Clapeyron:
$T_B = \Bigg(\frac{\,R\,\ln(P_0)}{\Delta H_{vap}}+\frac{1}{T_0}\Bigg)^{-1}$

donde:
$T B$	=Punto de ebullición normal en Kelvin
$R$	= Constante	$T 0$	= La temperatura dada en Kelvin
	= logaritmo en base e El aumento o ascenso ebulloscópico es el aumento del punto de ebullición que experimenta un disolvente puro, al formar una disolución con un soluto determinado. La magnitud del ascenso ebulloscópico, $\Delta\mathit{T}_b \$ , se obtiene al calcular la diferencia entre la temperatura de ebullición de la disolución y del disolvente puro, $\mathit{T}_b\$ y $\mathit{T}_b^* \$ respectivamente: $\Delta\mathit{T}_b = \mathit{T}_b - \mathit{T}_b^* \$ Es directamente proporcional a la molaridad del soluto, o más precisamente, a la actividad del soluto, según la siguiente ecuación: aumento ebulloscópico= i x K_b x actividad la actividad se expresa en mol/kg y se obtiene multiplicando la molalidad por el coeficiente de actividad. K_b, constante de aumento ebulloscópico, característica de cada sustancia. i es el factor de van't Hoff (ver Jacobus Henricus van't Hoff), tiene en cuenta la formación de iones en la solución, indica el número de partículas formadas por cada partícula de soluto que pasa a la solución. Por ejemplo: i = 1 para azúcar en agua. i = 2 para NaCl en agua (un ion cloruro y un ion sodio). i = 3 para CaCl₂ en agua (dos iones cloruro y un ion calcio). i = 2 para HCl en agua (se disocia completamente). i = 1 para HCl en benceno. (no se disocia en benceno)

http://www.buenastareas.com/ensayos/Punto-De-Congelacion/1056096.html
http://es.wikipedia.org/wiki/Punto_de_congelaci%C3%B3n
Gillespie, R. J. (1990). Química (II) (1.ª edición). Barcelona: Reverté. pp. 607. ISBN 84-291-7188-6.
↑ American Chemical Society, ed (2005). Química: Un proyecto de la American Chemical Society. Barcelona: Reverté. pp. 558-560. ISBN 8429170014. http://books.google.es/books?id=_FJ8ljXZD7IC&hl=es.
↑ Cifuentes, J. L. et ál. (2003). El océano y sus recursos. III: Las Ciencias del Mar- Oceanografía Física, matemáticas e ingeniería (3.ª edición). México: Fondo de Cultura Económica. ISBN 9681669533. http://books.google.es/books?id=ZHr_WjwT3c4C&hl=es.
↑ Morris, J. Gareth (1982). Fisicoquímica para biologos. Reverte. pp. 82. ISBN 8429118020. http://books.google.es/books?id=bKXHOvnJJXcC&printsec=frontcover&source=gbs_v2_summary_r&cad=0#v=onepage&q=&f=false. Consultado el 23 de enero de 2010.
↑ Hill, Richard W. (1980). Fisiología animal comparada: Un enfoque ambiental. Reverte. ISBN 8429118292. http://books.google.es/books?id=w7aoEY-_48EC&hl=es.
↑ Kiehl, Katie. University of Michigan (ed.): «Rana sylvatica» (en inglés). Animal Diversity Web. Consultado el 7 de noviembre de 2009.
↑ Muir Timothy J; Costanzo Jon P; Lee Richard E. (2007). «Osmotic and metabolic responses to dehydration and urea-loading in a dormant, terrestrially hibernating frog» (en inglés). Journal of Comparative

Experimental Physical Chemistry

miércoles, 2 de noviembre de 2011

PUNTO DE CONGELACIÓN Y EBULLICIÓN